Människor använder decimala (bas 10) talsystem för räkning och mätningar (förmodligen för att vi har 10 fingrar). Datorer använder binära (bas 2) talsystem, eftersom de är gjorda av binära digitala komponenter (kända som transistorer) som fungerar i två tillstånd – på och av. I beräkningar använder vi också hexadecimala (bas 16) eller oktala (bas 8) talsystem, som en kompakt form för att representera binära tal.
Decimaltal (bas 10) talsystem
Decimaltalsystemet har tio symboler: 0, 1, 2, 3, 4, 5, 6, 7, 8 och 9, så kallade siffror. Den använder positionsbeteckning. Det vill säga, den minst signifikanta siffran (siffran längst till höger) är av storleksordningen 100 (enheter), den andra siffran längst till höger är av storleksordningen 101 (tiotal), den tredje höger- de flesta siffror är av storleksordningen 102 (hundratals), och så vidare. Till exempel,
735 = 700 + 30 + 5 = 7×102 + 3×101 + 5×100
Vi ska beteckna ett decimaltal med ett index 10. Till exempel 73510
Binärt (bas 2) talsystem
Binärt talsystem har två symboler: 0 och 1, kallade bitar. En binär siffra kallas en bit och åtta bitar kallas en byte eller oktett. Det binära talsystemet är också en positionsbeteckning, t.ex.
101102 = 10000 + 0000 + 100 + 10 + 0 = 1×24 + 0×23 + 1×22 + 1×21 + 0×20
Vissa programmeringsspråk betecknar binära tal med prefixet 0b eller 0B (t.ex. 0b1001000), eller prefixet b med bitarna citerade (t.ex. b’10001111′).
Hexadecimalt talsystem (bas 16)
Hexadecimalt talsystem använder 16 symboler: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E och F, så kallade hexadecimala siffror. Det är en positionsbeteckning, t.ex.
A3E16 = AOO + 30 + E = 10×162 + 3×161 + 14×160
Vissa programmeringsspråk betecknar hexadecimalt tal med prefixet 0x eller 0X (t.ex. 0x1A3C5F), eller prefixet x med hexadecimala siffror angivna (t.ex. x’C3A4D98B’). De flesta programmeringsspråk accepterar gemener ”a” till ”f” samt versaler ”A” till ”F”. Observera att varje hexadecimal siffra är ekvivalent med 4 binära bitar, dvs. förkortning för 4 bitar, enligt följande tabell:
| Hexadecimal | Binär | Decimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
Heltalsrepresentation
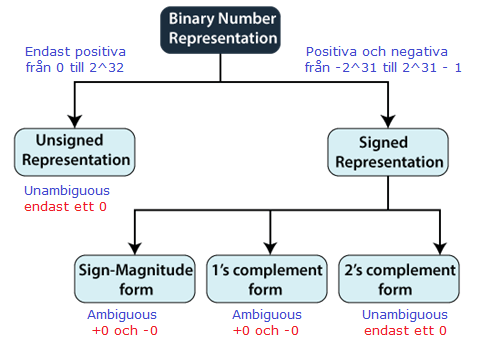
Heltal i det binära talsystemet representeras som signerat och osignerat format.
- Med signerat format menas att den första biten i det binära talet markerar om talet är positivt eller negativt. Till exempel i talet 10010011 är den första biten som säger till att talet är negativt. Om biten hade varit istället 0, så var talet positivt.
- Med osignerat format menas endast positiva tal utan någon tecken före. I osignerat format finns alltid 0 som positivt nummer.
Det är väldigt enkelt att representera positiva och negativa tal i vårt dagliga liv. Vi använder positiva tal utan något tecken före och vi använder minustecknet före för negativa tal. Men i det digitala systemet är det inte möjligt att använda negativa tecken framför talet eftersom talet är i binär form. För att representera tecknet i binära tal behöver vi en speciell notation.
Signerade binära tal
Signerade binära tal representeras på tre sätt:
- Signerad-Magnitud – Ett binärt tal markeras med en bit, 0 positiv, 1 negativ. Förutom denna teckenbit representerar n-1-bitar storleken på talet.
- Första komplement – Genom att invertera varje bit av ett tal kan vi få första komplement av ett tal. Negativa tal kan representeras som första komplement och en extra bit precis som signerad-magnitud.
- Andra komplement – Genom att invertera varje bit av ett tal och addera en 1 till den minsta signifikant delen får man det andra komplementet. För att markera ett tal som positivt eller negativt används den första bit i den mest signifikant delen i talet.
Första komplement
Första komplement används främst för att representera signerade binära tal. Förutom det används första komplement i aritmetiska operationer såsom addition och subtraktion.
Exempel 1 – Med åtta bitar representera +6 och -6 med första komplement
- +6 = 610 = 000001102 Första biten markerar talet som positivt, ingenting behöver göras.
- -6 = -610 = –000001102 Här behöver användas första komplementet. 00000110 inverteras 11111001 (representerar –000001102). Minustecknet behövs inte längre.
Exempel 2 – Med åtta bitar och första komplement addera 4810 med -1910
- 4810 = 001100002
- -1910 = –000100112
- Att använda minustecknet går det inte i en dators matematik därför används här första komplement 00010011 inverteras 11101100
- Nu kan subtraktionen (4810 ) – (-1910 ) skrivas om istället som addition så här: 001100002 + 111011002
Nu kan additionen räknas ut och för att förstå bättre det använder jag en tabell:
- Första och andra rad är en del av tabellen.
- Tredje rad är tom
- Fjärde rad är carry (bärare)
- Femte rad är 4810 i binärt
- Sjätte rad är första komplement för 1910
- Sjunde rad är tom
- Åttonde rad är additionens resultat
- I nionde rad adderas en 1 för att korrigera resultatet (carry)
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | |||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||
| carry | 1 | 1 | 1 | |||||||
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | |||
| + | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |||
| + | 1 | |||||||||
| 48 – 19 = 29 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
Andra komplement
På liknande sätt som första komplement representeras negativa tal med hjälp av talets komplement. Skillnaden är att 1 adderas alltid till komplementet.
Exempel 2 – Med åtta bitar och andra komplement addera 2310 med -910
- 2310 = 000101112
- -910 = –000010012
- –000010012 inverteras 11110110
- 11110110 + 1 = 11110111
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | |||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||
| out | in | |||||||||
| carry in = out, no overflow | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
| carry ignoreras | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | ||
| + | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ||
| 23 – 9 = 14 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |