Om vi använder en miniräknare och multiplicerar två stora decimala tal med varandra visar miniräknaren bokstaven E bland siffrorna i resultatet:
290 345 897 234 x 85 776 445 069 803 345 = 2,490483891E28
- E står för Exponent och den representerar talsystemets basen, det vill säga 10.
- Basen höjs upp till en viss exponent, i exemplet 28
- Talet 2,490483891E28 kan betecknas så här: 2,490483891*1028
I samma tal får kommatecken flyttas antingen till vänster eller till höger men för att inte ändra talets värde höjer eller minskar man exponenten.
- Till exempel om kommatecknet flyttas två steg åt höger kommer exponenten att minska med samma värde: 249,0483891*1026
- Kommatecknet kan också flyttas åt vänster och då ska exponenten öka i stället: 0,02490483891*1030
Att få flytta kommatecknet gör att talet betraktas vara FLYTTAL som på engelska kallas för ”floating point numbers”.
När man pratar om bitar och det binära talet kan tabellen nedan vara användbart:
| 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | . | 2-1 | 2-2 | 2-3 | 2-4 | 2-5 | 2-6 |
| 1/2 | 1/4 | 1/8 | 1/16 | 1/32 | 1/64 | |||||||||||
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 0.5 | 0.25 | 0.125 | 0.0625 | 0.03125 | 0.015625 |
IEEE 754
Hur kan flyttal representeras som en följd av ettor och nollor? Till exempel hur ska följande tal -1.5*103 och -1.1×23 representeras med ettor och nollor?
Först ska talen konverteras till binära. Därefter läggs till konverterade talen antingen en 1 eller en 0 beroende om talen är negativa eller positiva. Basen (radix) och Exponenten ska också representeras med ettor och nollor samt decimaldelen (mantissa).
Det finns flera olika sätt att representera flyttal och för att kunna ha gemensamt uppfattning på hur flyttal kan hanteras har standardiseringsorganisationen IEEE arbetat fram en standard som heter IEEE 754. Standarden kan illustreras så här:
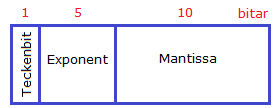
Antal bitar att använda för att representera jätte stora eller små tal avgör precisionen. Ju fler bitar man använder desto större och mer precisa tal kan representeras. Här nedan några precisionsmetoder:
- Halv precision: 16 bitar (1 tecken bit, 5 exponentbitar och 10 bitar för mantissa.)
- Enkel precision: 32 bitar (1 tecken bit, 8 exponentbitar och 23 bitar för mantissa.)
- Dubbel precision: 64 bitar (1 tecken bit, 11 exponentbitar och 52 bitar för mantissa.)